Computability Theory - Decidability(Decidable Languages)
Computability Theory - Decidability - Decidable Languages
Intro
We know Church-Turing thesis essentially says that the notion of algorithm are equivalent to Turing machine(TM). A TM can simulate a computer by simulating the basic operations like addition, multiplication, division, etc. A computer can also simulate a TM to keep track of tape contents by using programming languages like Python.
If a TM cannot solve a problem, that means a computer can also not solve that problem. When we say "cannot solve a problem" in previous sentence. The words solve means there is no decider for a given Language $L$.
Here, no decider doesn't means no recognizer.
Can Turing machine answer questions about what other machines(DFAs, for example) can do/be solved?
- We can build up to Turing machines which allows us to show that a problem can be solved.
That's what what this article will show next.
Decidable Languages
Representation / Encoding
A string representation/encoding of machine $M$ can be written as $\langle M \rangle$.
Acceptance problem for DFA
The acceptance problem for DFAs of testing whether a particular DFA accepts a given string can be expressed as a language, $A_{DFA}$.
$$ A_{DFA} = \{ \langle B,w \rangle \mid B \text{ is a DFA that accepts input string } w\} $$
- $A$ states for an acceptance problem.
- $\langle B,w \rangle$ means whether some string encoding of a DFA $B$ accepts an input $w$.
Overall, it means the problem of testing whether a DFA $B$ accepts an input $w$ is the same as the problem of testing whether $\langle B,w \rangle \in A_{DFA}$.
Theorem:
$A_{DFA}$ is decidable. (In another words, a TM exists for $A_{DFA}$ that always halts)
Proof:
$M$ = "On input $\langle B,w \rangle$, where $B$ is a DFA and $w$ is a string:
- Simulate $B$ on input $w$.
- If the simulation($B$) ends in an accept state, $M$ accepts. If it ends in a non-accept state, $M$ reject."
Note: $M$ is a Turing machine, and $M$ is a decider for $A_{DFA}$. It's important to understand only a language can be decidable, a machine is a decider.
Acceptance problem for NFA
$$ A_{NFA} = \{ \langle B,w \rangle \mid B \text{ is a NFA that accepts input string } w\} $$
Theorem:
$A_{NFA}$ is decidable.
Proof:
$N$ = "On input $\langle B, w \rangle$, where $B$ is a NFA and $w$ is a string:
- Convert NFA $B$ to an equivalent DFA $C$.
- Run the Turing machine $M$ for $A_{DFA}$ on $\langle C, w \rangle$
- If $M$ accepts, accept; otherwise, reject." (Output whatever the Turing machine $M$ says)
Note 01: In step #2, it is important to know when we send something to machine $M$. Let's for example $\langle X, x \rangle$, $X$ has to be a DFA(NOT an NFA or something else). It is because we defined that in problem "Acceptance problem for DFA".
Note 02: The reason why we need convert a DFA to a NFA is because a NFA may includes $\epsilon$ transition. So, it may ends up with a loop and run forever.
Acceptance problem for REX
$$ A_{REX} = \{ \langle R,w \rangle \mid R \text{ is a regular expression that generates string } w\} $$
Theorem:
$A_{REX}$ is decidable.
Proof:
$P$ = "On input $\langle R, w \rangle$, where $R$ is a regular expression and $w$ is a string:
- Convert regular expression $R$ to an equivalent NFA $A$.
- Run TM $N$ on input $\langle A, w \rangle$
- If $N$ accepts, accept; if $N$ rejects, reject."
Emptiness problem for DFA
$$ E_{DFA} = \{ \langle A \rangle \mid A \text{ is a DFA and } L(A) = \empty\} $$
- $E$ states for an emptiness problem.
Overall, it means whether a DFA $A$ accepts nothing(no accepting string in language $A$).
Theorem:
$E_{DFA}$ is decidable.
Proof:
$T$ = "On input $\langle A \rangle$, where $A$ is a DFA:
- Mark the start state of $A$.
Repeat until no new states get marked:
- Mark any state that has a transition coming into it from any state that is already marked.
- If no accept state is marked, accept; otherwise, reject."
Note: A naive way to think about this problem is by looking at, if DFA $A$ has a final states. That is NOT true. A DFA can have a unreachable final states, which has a final states but accepting nothing.
A right way to think of the problem is that if there exists a set of transitions allow us to reach final state.
Equality problem for DFA
$$ EQ_{DFA} = \{ \langle A,B \rangle \mid A \text{ and } B \text{ are DFAs and } L(A) = L(B)\} $$
Theorem:
$EQ_{DFA}$ is decidable.
Proof:
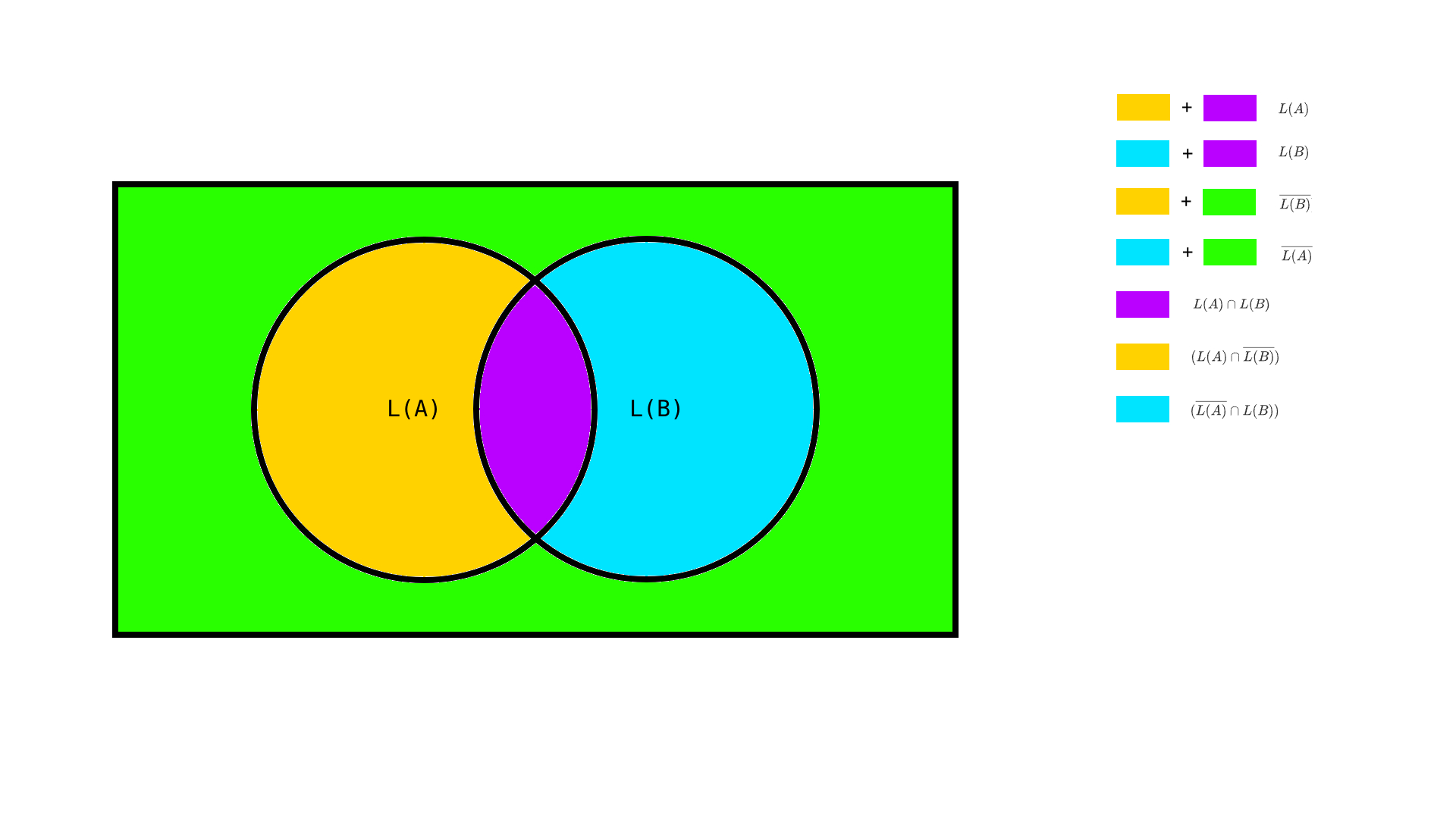
$$ L(C) = (L(A)\cap \overline{L(B)}) \cup (\overline{L(A)} \cap L(B)) $$
$F$ = "On input $\langle A,B \rangle$, where $A$ and $B$ are DFAs:
- Construct DFA $C$ as described.
- Run TM $T$ on input $\langle C \rangle$.
- If $T$ accepts, accept. If $T$ rejects, reject."
It's important to understand the idea behind the proof algorithm:
$$ \langle A,B \rangle \in EQ_{DFA} \iff L(A) = L(B) \\ \iff L(A) \subseteq L(B) \text{ AND } L(B) \subseteq L(A) $$
We also know:
$$ L(A) \subseteq L(B) \iff L(A) \cap \overline{L(B)} = \empty \\ L(B) \subseteq L(A) \iff L(B) \cap \overline{L(A)} = \empty $$
That's how we got $L(C)$:
$$ L(C) = (L(A)\cap \overline{L(B)}) \cup (\overline{L(A)} \cap L(B)) $$
Acceptance problem for CFG
$$ A_{CFG} = \{ \langle G,w \rangle \mid G \text{ is a CFG that accepts input string } w\} $$
Theorem:
$A_{CFG}$ is decidable.
This implies $A_{PDA}$ is also decidable, since we can convert a CFG into a PDA.
Proof:
$S$ = "On input $\langle G,w \rangle$, where $G$ is a CFG and $w$ is a string:
- Convert $G$ to an equivalent grammer $C$ in Chomsky normal form(CNF).
- If $w=\epsilon$, and $S \to \epsilon$ is a rule in $C$, accept; If $S \to \epsilon$ is a not rule in $C$, reject.
- let $n$ be the length of string $w$.
- Generate all possible derivations of $2n-1$.
- If any of the dervations result in $w$, accept; otherwise, reject"
Acceptance problem for CFL
$$ A_{CFL} = \{ \langle G,w \rangle \mid G \text{ is a CFL that accepts input string } w\} $$
Theorem:
$A_{CFL}$ is decidable.
Proof:
$M_G$ = "On input $w$:
- Run TM $S$ on input $ \langle G,w \rangle$.
- If this machine accepts, accept; if it rejects, reject"
Emptiness problem for CFG
$$ E_{CFG} = \{ \langle G \rangle \mid G \text{ is a CFG and } L(G) = \empty\} $$
Theorem:
$E_{CFG}$ is decidable.
Proof:
$R$ = "On input $\langle G \rangle$, where $G$ is a CFG:
- Mark all terminal symbols in $G$.
Repeat until no new variables get marked:
- Mark any variable $A$ where $G$ has a rule $A \to U_1 U_2 ... U_k$ and each symbol $U_1, ..., U_k$ has already marked.
- If the start variable is not marked, accept; otherwise, reject."
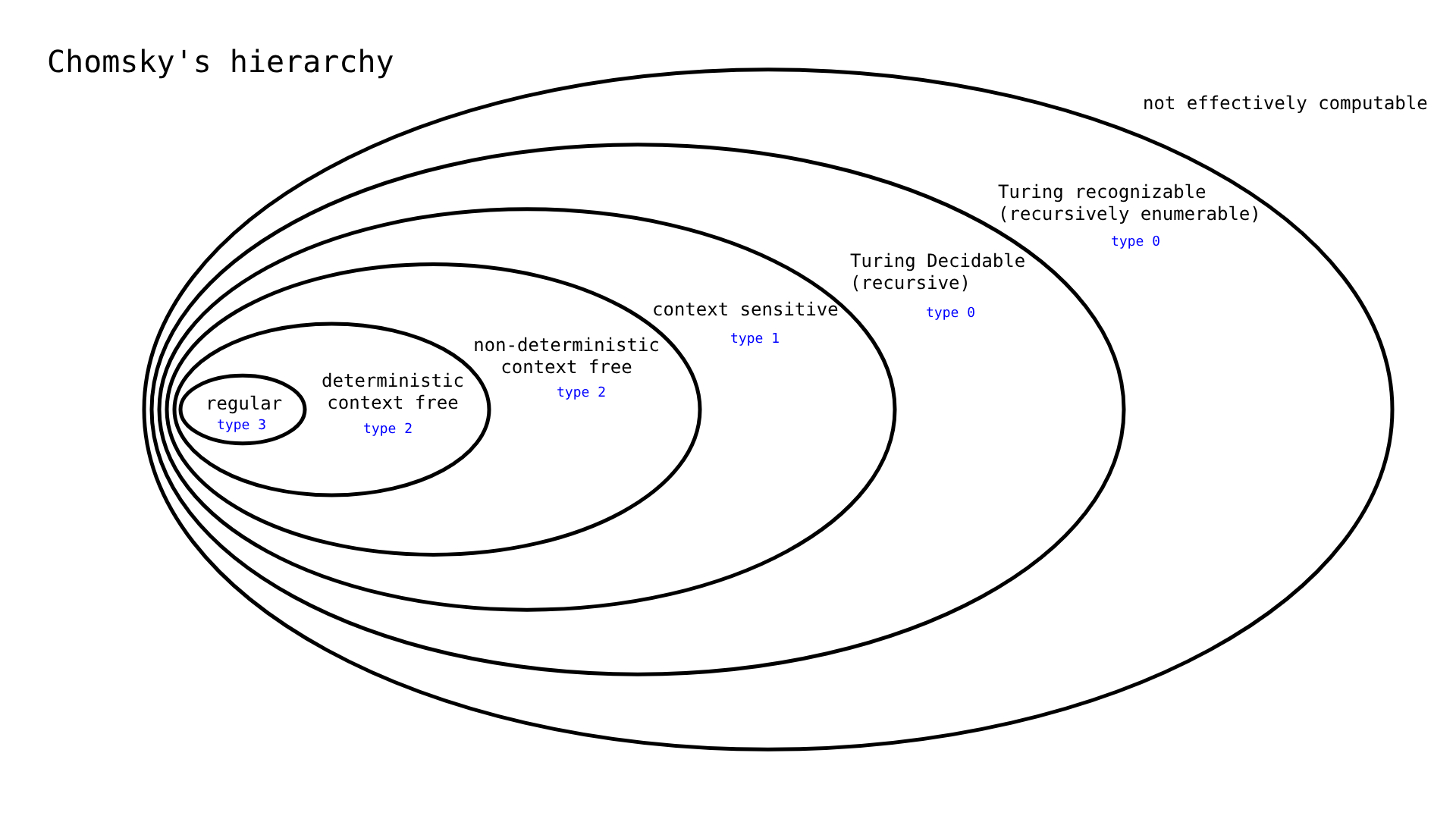
Chomsky Hierarchy
Summary
| TM | Languages / Problems |
|---|---|
| $M$ | $A_{DFA} = \{ \langle B,w \rangle \mid B \text{ is a DFA that accepts input string } w\}$ |
| $N$ | $A_{NFA} = \{ \langle B,w \rangle \mid B \text{ is a NFA that accepts input string } w\}$ |
| $P$ | $A_{REX} = \{ \langle R,w \rangle \mid R \text{ is a regular expression that generates string } w\}$ |
| $T$ | $E_{DFA} = \{ \langle A \rangle \mid A \text{ is a DFA and } L(A) = \empty\}$ |
| $O$ | $ALL_{DFA} = \{ \langle A \rangle \mid A \text{ is a DFA and } L(A) = \Sigma^{*}\}$ |
| $F$ | $EQ_{DFA} = \{ \langle A,B \rangle \mid A \text{ and } B \text{ are DFAs and } L(A) = L(B)\}$ |
| $S$ | $A_{CFG} = \{ \langle G,w \rangle \mid G \text{ is a CFG that accepts input string } w\}$ |
| $M_G$ | $A_{CFL} = \{ \langle G,w \rangle \mid G \text{ is a CFL that accepts input string } w\}$ |
| $R$ | $E_{CFG} = \{ \langle G \rangle \mid G \text{ is a CFG and } L(G) = \empty\}$ |